The HM encoder applies a table to quickly get the number of fractional bits generated when a bin is coded with the current probability state p.
There are actually two tables in the source of HM. One which was probably obtained by experiments and another derived from the formula of entropy -lg(p) directly. In order to get a better understanding, I wrote a small tool that generates a very long sequence of bins/states to be coded. This sequence is encoded with CABAC twice: once only the sequence itself, the other time injecting a bin of probability state p in regular intervals. The difference in the resulting stream size is used to calculate the number of bits for bins in state p.
The number of bits/bin for each of these approaches are depicted in the following two figures.
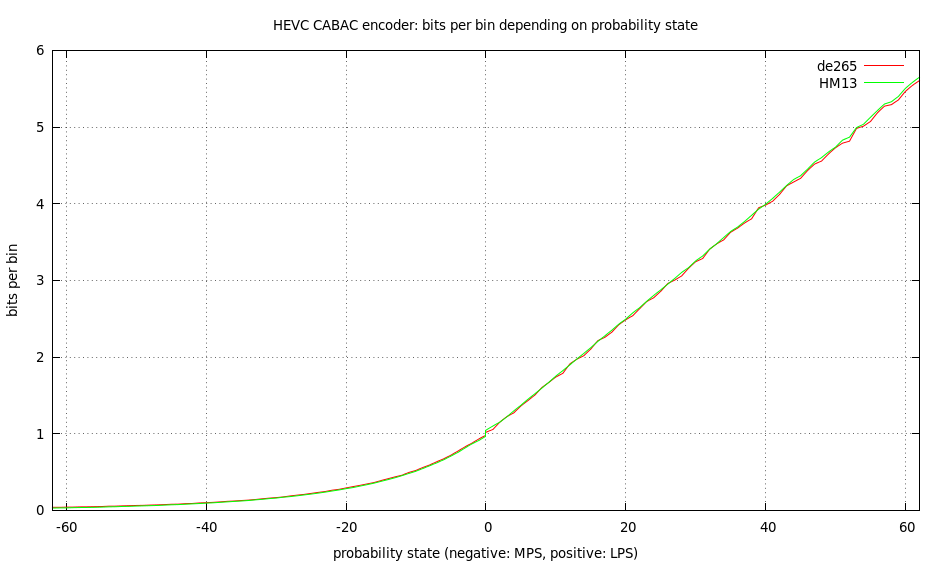

In order to measure the accuracy of the model, I recorded the sequence of bins of a real, long HEVC coded movie and encoded this sequence with a real CABAC encoder and computed the estimates, too.
I found that the HM13 table is off by 0.43%, while the directly computed table of HM13 (which is not used), is off by 0.52%. However, the table I computed is only off by 0.07%.
It appears that the "bumps" in the diagrams are actually real because of the limited resolution of the CABAC encoder and they are no artifact of the estimation process.
Ref:https://github.com/strukturag/libde265/wiki/CABAC-entropy-estimation
There are actually two tables in the source of HM. One which was probably obtained by experiments and another derived from the formula of entropy -lg(p) directly. In order to get a better understanding, I wrote a small tool that generates a very long sequence of bins/states to be coded. This sequence is encoded with CABAC twice: once only the sequence itself, the other time injecting a bin of probability state p in regular intervals. The difference in the resulting stream size is used to calculate the number of bits for bins in state p.
The number of bits/bin for each of these approaches are depicted in the following two figures.


In order to measure the accuracy of the model, I recorded the sequence of bins of a real, long HEVC coded movie and encoded this sequence with a real CABAC encoder and computed the estimates, too.
I found that the HM13 table is off by 0.43%, while the directly computed table of HM13 (which is not used), is off by 0.52%. However, the table I computed is only off by 0.07%.
It appears that the "bumps" in the diagrams are actually real because of the limited resolution of the CABAC encoder and they are no artifact of the estimation process.
Ref:https://github.com/strukturag/libde265/wiki/CABAC-entropy-estimation
No comments:
Post a Comment